大学入学共通テスト（理科） 過去問
令和4年度（2022年度）本試験
問1 (物理基礎（第1問） 問1)
問題文
次の文章中の空欄（ ア ）・（ イ ）に入れる数値の組合せとして最も適当なものを、次の選択肢のうちから一つ選べ。
図1のように、隣りあって平行に敷かれた線路上を、2台の電車（電車AとB）が、反対向きに等速直線運動をしながらすれちがう。電車AとBの長さは、それぞれ、50mと100mであり、電車AとBの速さは、それぞれ、10m／sと15m／sである。電車Aに対する電車Bの相対速度の大きさは（ ア ）m／sである。また、電車Aの先頭座席に座っている乗客の真横に、
電車Bの先頭が来てから電車Bの最後尾が来るまでに要する時間は（ イ ）sである。
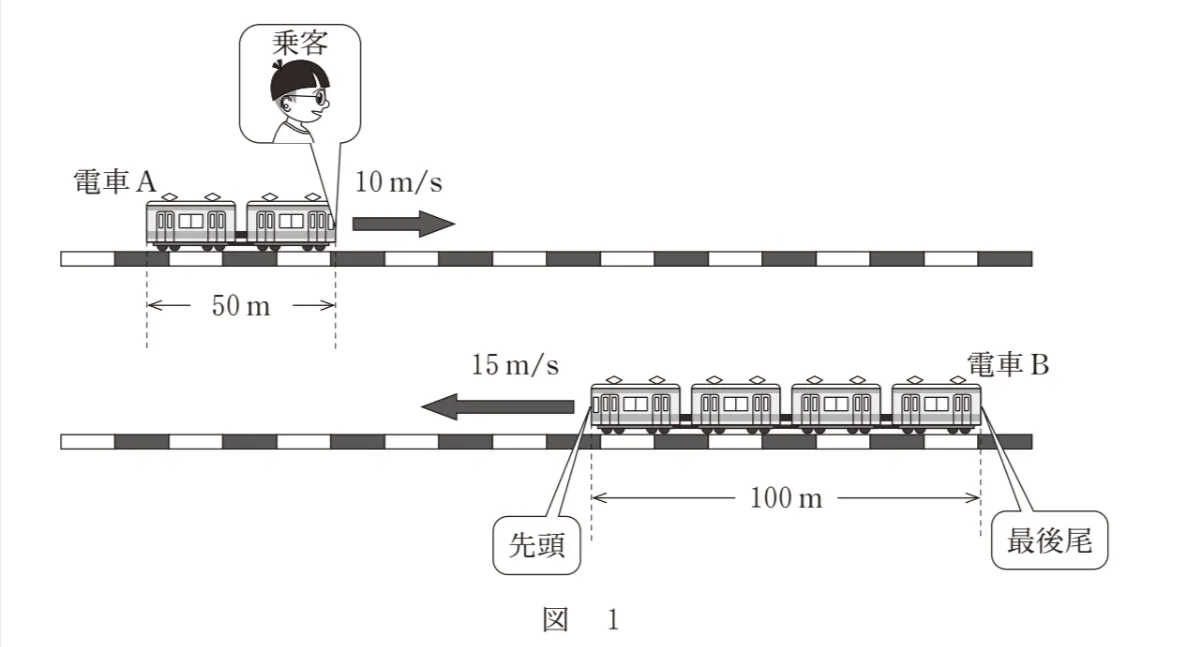
図1のように、隣りあって平行に敷かれた線路上を、2台の電車（電車AとB）が、反対向きに等速直線運動をしながらすれちがう。電車AとBの長さは、それぞれ、50mと100mであり、電車AとBの速さは、それぞれ、10m／sと15m／sである。電車Aに対する電車Bの相対速度の大きさは（ ア ）m／sである。また、電車Aの先頭座席に座っている乗客の真横に、
電車Bの先頭が来てから電車Bの最後尾が来るまでに要する時間は（ イ ）sである。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（理科）試験 令和4年度（2022年度）本試験 問1（物理基礎（第1問） 問1） （訂正依頼・報告はこちら）
次の文章中の空欄（ ア ）・（ イ ）に入れる数値の組合せとして最も適当なものを、次の選択肢のうちから一つ選べ。
図1のように、隣りあって平行に敷かれた線路上を、2台の電車（電車AとB）が、反対向きに等速直線運動をしながらすれちがう。電車AとBの長さは、それぞれ、50mと100mであり、電車AとBの速さは、それぞれ、10m／sと15m／sである。電車Aに対する電車Bの相対速度の大きさは（ ア ）m／sである。また、電車Aの先頭座席に座っている乗客の真横に、
電車Bの先頭が来てから電車Bの最後尾が来るまでに要する時間は（ イ ）sである。
図1のように、隣りあって平行に敷かれた線路上を、2台の電車（電車AとB）が、反対向きに等速直線運動をしながらすれちがう。電車AとBの長さは、それぞれ、50mと100mであり、電車AとBの速さは、それぞれ、10m／sと15m／sである。電車Aに対する電車Bの相対速度の大きさは（ ア ）m／sである。また、電車Aの先頭座席に座っている乗客の真横に、
電車Bの先頭が来てから電車Bの最後尾が来るまでに要する時間は（ イ ）sである。
- ア：5 イ：20
- ア：5 イ：30
- ア：10 イ：10
- ア：10 イ：15
- ア：15 イ：6.7
- ア：15 イ：10
- ア：25 イ：4.0
- ア：25 イ：6.0
正解！素晴らしいです
残念...
この過去問の解説
令和4年度（2022年度）本試験 問題一覧
次の問題（問2）へ