大学入学共通テスト(理科) 過去問
令和5年度(2023年度)本試験
問84 (物理(第2問) 問5(1))
問題文
空気中での落下運動に関する探究について、次の問いに答えよ。
生徒:抵抗力の大きさRが速さvに比例すると仮定すると、正の比例定数kを用いて
R=kv
と書けます。物体の質量をm、重力加速度の大きさをgとすると、R=mgとなるvが終端速度の大きさvfなので、
vf=mg/k
と表されます。実験をしてvfとmの関係を確かめてみたいです。
先生:いいですね。図1のようなお弁当のおかずを入れるアルミカップは、何枚か重ねることによって質量の異なる物体にすることができるので、落下させてその関係を調べることができますね。その物体の形は枚数によらずほぼ同じなので、kは変わらないとみなしましょう。物体の質量mはアルミカップの枚数nに比例します。
生徒:そうすると、vfがnに比例することが予想できますね。
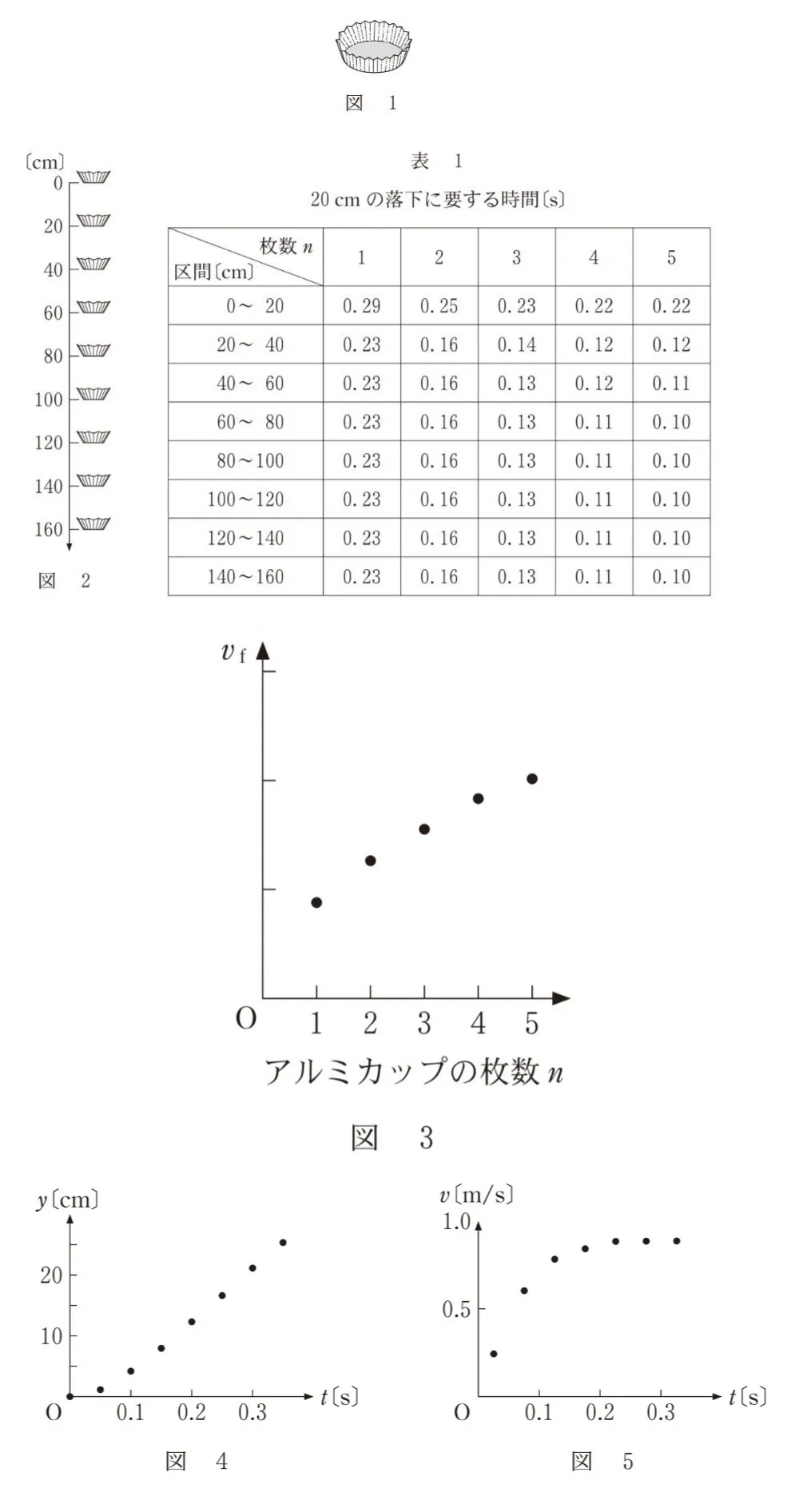
n枚重ねたアルミカップを落下させて動画を撮影した。図2のように、アルミカップが落下していく途中で、20cmごとに落下するのに要する時間を10回測定して平均した。この実験をn=1、2、3、4、5の場合について行った。その結果を表1にまとめた。
生徒:アルミカップの枚数nとvfの測定値を図3に点で描き込みましたが、
vf=mg/kに基づく予想と少し違いますね。
先生:実は、物体の形状や速さによっては、空気による抵抗力の大きさRは、速さに比例するとは限らないのです。
生徒:そうなんですか。授業で習ったvfの式は、いつも使えるわけではないのですね。
先生:はい。ここでは、Rがv2に比例するとみなせる場合も考えてみましょう。正の比例定数k′を用いてRを
R=k′v2
と書くと、先ほどと同様に、R=mgとなるvが終端速度の大きさvfなので、
vf=√mg/k′
と書くことができます。比例定数kと同様に、k′はnによって変化しないものとみなしましょう。mはnに比例するので、vfとnの関係を調べると、R=kvとR=k′v2のどちらが測定値によく合うかわかります。
生徒:わかりました。縦軸と横軸をうまく選んでグラフを描けば、原点を通る直線になってわかりやすくなりますね。
先生:それでは、そのグラフを描いてみましょう。
先生:抵抗力の大きさRと速さvの関係を明らかにするために、ここまでは終端速度の大きさと質量の関係を調べましたが、落下途中の速さが変化していく過程で、Rとvの関係を調べることもできます。鉛直下向きにy軸をとり、アルミカップを原点から初速度0で落下させます。アルミカップの位置yをΔt=0.05sごとに記録したところ、図4のようなy―tグラフが得られました。このy―tグラフをもとにして、Rとvの関係を調べる手順を考えてみましょう。
この手順を説明する文章中の( エ )に入れる記述として最も適当なものを、後の選択肢のうちから一つ選べ。
まず、図4のy―tグラフより、Δt=0.05sごとの平均の速さvを求め、図5のv―tグラフをつくる。次に、加速度の大きさaを調べるために、( エ )。
こうして求めたaから、アルミカップにはたらく抵抗力の大きさRは、R=( オ )と求められる。
以上の結果をもとに、Rとvの関係を示すグラフを描くことができる。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(理科)試験 令和5年度(2023年度)本試験 問84(物理(第2問) 問5(1)) (訂正依頼・報告はこちら)
空気中での落下運動に関する探究について、次の問いに答えよ。
生徒:抵抗力の大きさRが速さvに比例すると仮定すると、正の比例定数kを用いて
R=kv
と書けます。物体の質量をm、重力加速度の大きさをgとすると、R=mgとなるvが終端速度の大きさvfなので、
vf=mg/k
と表されます。実験をしてvfとmの関係を確かめてみたいです。
先生:いいですね。図1のようなお弁当のおかずを入れるアルミカップは、何枚か重ねることによって質量の異なる物体にすることができるので、落下させてその関係を調べることができますね。その物体の形は枚数によらずほぼ同じなので、kは変わらないとみなしましょう。物体の質量mはアルミカップの枚数nに比例します。
生徒:そうすると、vfがnに比例することが予想できますね。
n枚重ねたアルミカップを落下させて動画を撮影した。図2のように、アルミカップが落下していく途中で、20cmごとに落下するのに要する時間を10回測定して平均した。この実験をn=1、2、3、4、5の場合について行った。その結果を表1にまとめた。
生徒:アルミカップの枚数nとvfの測定値を図3に点で描き込みましたが、
vf=mg/kに基づく予想と少し違いますね。
先生:実は、物体の形状や速さによっては、空気による抵抗力の大きさRは、速さに比例するとは限らないのです。
生徒:そうなんですか。授業で習ったvfの式は、いつも使えるわけではないのですね。
先生:はい。ここでは、Rがv2に比例するとみなせる場合も考えてみましょう。正の比例定数k′を用いてRを
R=k′v2
と書くと、先ほどと同様に、R=mgとなるvが終端速度の大きさvfなので、
vf=√mg/k′
と書くことができます。比例定数kと同様に、k′はnによって変化しないものとみなしましょう。mはnに比例するので、vfとnの関係を調べると、R=kvとR=k′v2のどちらが測定値によく合うかわかります。
生徒:わかりました。縦軸と横軸をうまく選んでグラフを描けば、原点を通る直線になってわかりやすくなりますね。
先生:それでは、そのグラフを描いてみましょう。
先生:抵抗力の大きさRと速さvの関係を明らかにするために、ここまでは終端速度の大きさと質量の関係を調べましたが、落下途中の速さが変化していく過程で、Rとvの関係を調べることもできます。鉛直下向きにy軸をとり、アルミカップを原点から初速度0で落下させます。アルミカップの位置yをΔt=0.05sごとに記録したところ、図4のようなy―tグラフが得られました。このy―tグラフをもとにして、Rとvの関係を調べる手順を考えてみましょう。
この手順を説明する文章中の( エ )に入れる記述として最も適当なものを、後の選択肢のうちから一つ選べ。
まず、図4のy―tグラフより、Δt=0.05sごとの平均の速さvを求め、図5のv―tグラフをつくる。次に、加速度の大きさaを調べるために、( エ )。
こうして求めたaから、アルミカップにはたらく抵抗力の大きさRは、R=( オ )と求められる。
以上の結果をもとに、Rとvの関係を示すグラフを描くことができる。

-
v―tグラフのすべての点のできるだけ近くを通る一本の直線を引き、その傾きを求めることによってaを求める。|
-
v―tグラフから終端速度を求めることによってaを求める。
- v―tグラフからΔtごとの速度の変化を求めることによってa―tグラフをつくる。
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
解答 v―tグラフからΔtごとの速度の変化を求めることによってa―tグラフをつくる。
解説 図5から加速度を求める方法を問う問題です。
選択肢を1つずつ確認してみましょう。
v―tグラフのすべての点のできるだけ近くを通る一本の直線を引き、その傾きを求めることによってaを求める。|
誤答選択肢です。
等加速度直線運動の場合であればこの方法で加速度を
求められますが、図5は等加速度直線運動のv-tグラフでは
ないので不適切です。
v―tグラフから終端速度を求めることによってaを求める。
誤答選択肢です。
終端速度は加速度がゼロになった状態の速度です。
終端速度に到達する前の加速度を
この情報から求めることはできません。
この選択肢が正解となります。
速度の変化v(t+Δt)-v(t)をΔtで割ることで
加速度を求められるため、この選択肢が適切です。
参考になった数0
この解説の修正を提案する
前の問題(問82)へ
令和5年度(2023年度)本試験 問題一覧
次の問題(問85)へ