大学入学共通テスト(理科) 過去問
令和6年度(2024年度)本試験
問74 (物理(第2問) 問5)
問題文
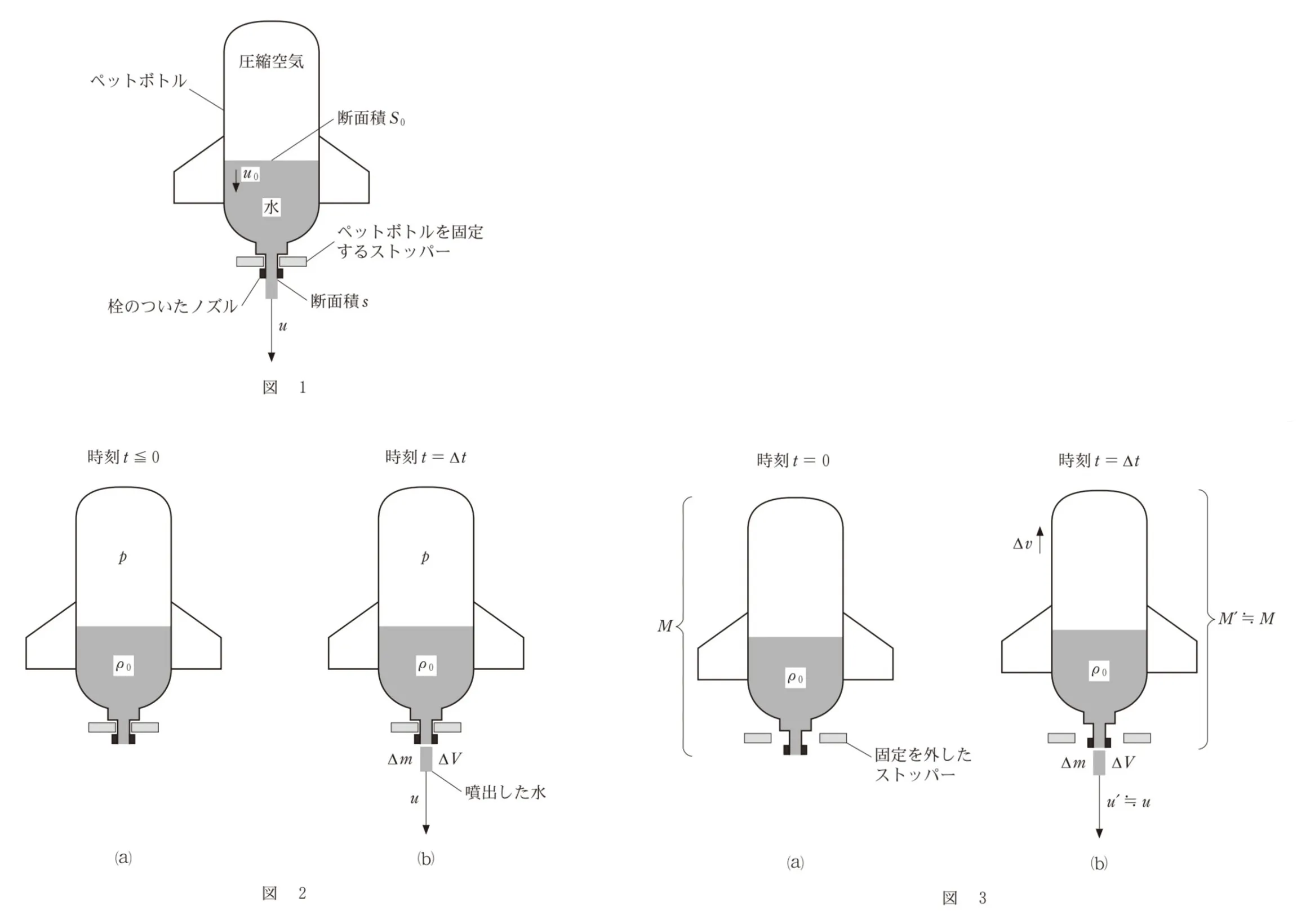
図1は、ペットボトルロケットの模式図である。ペットボトルの飲み口には栓のついた細い管(ノズル)が取り付けられていて、内部には水と圧縮空気がとじこめられている。ノズルの栓を開くとその先端から下向きに水が噴出する。ペットボトルとノズルはそれぞれ断面積S0、sの円筒形とする。考えやすくするために、以下の計算では、水の運動による摩擦(粘性)、空気抵抗、大気圧、重力の影響は無視する。
図1のように、ペットボトルがストッパーで固定されている場合を考える。
栓を開けた後、図2(a)のような状態にあったところ、時刻t=0からt=△tまでの間に質量△m、体積△Vの水が噴出し、図2(b)のような状態になった。このとき、△tは小さいので、t=0からt=△tまでの間、圧縮空気の圧力pや、噴出した水の速さuは一定とみなせるものとする。また、ペットボトルやノズルの中にあるときの水の運動エネルギーは考えなくてよい。水の密度をρ0とする。なお、以下の図で、t<0で噴出した水は省略されている。
今度は、ペットボトルロケットが静止した状態から飛び出す状況を考える。時刻t<0では、図2(a)と同じ状態であり、t=0にストッパーを外して動けるようになったとする(図3(a))。t=△tでは、水を噴出したロケットは上向きに動いている(図3(b))。t=0での、ペットボトルと内部の水やノズルを含むロケット全体の質量をM、速さを0とする。また、t=△tでの、ロケット全体の質量をM′、速さを△v、△tの間に噴出した水の速さをu′とする。△tが小さいときには、△mと△vも小さいので、M′をMに、u′をuに等しいとみなせるものとする。ペットボトル内部の水の流れの影響は考えなくてよいものとする。
時刻t=△tでのロケットの運動量と噴出した水の運動量の和は、t=0でのロケットの運動量に等しいと考えられる。その関係を表す式として最も適当なものを、次の選択肢のうちから一つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(理科)試験 令和6年度(2024年度)本試験 問74(物理(第2問) 問5) (訂正依頼・報告はこちら)
図1は、ペットボトルロケットの模式図である。ペットボトルの飲み口には栓のついた細い管(ノズル)が取り付けられていて、内部には水と圧縮空気がとじこめられている。ノズルの栓を開くとその先端から下向きに水が噴出する。ペットボトルとノズルはそれぞれ断面積S0、sの円筒形とする。考えやすくするために、以下の計算では、水の運動による摩擦(粘性)、空気抵抗、大気圧、重力の影響は無視する。
図1のように、ペットボトルがストッパーで固定されている場合を考える。
栓を開けた後、図2(a)のような状態にあったところ、時刻t=0からt=△tまでの間に質量△m、体積△Vの水が噴出し、図2(b)のような状態になった。このとき、△tは小さいので、t=0からt=△tまでの間、圧縮空気の圧力pや、噴出した水の速さuは一定とみなせるものとする。また、ペットボトルやノズルの中にあるときの水の運動エネルギーは考えなくてよい。水の密度をρ0とする。なお、以下の図で、t<0で噴出した水は省略されている。
今度は、ペットボトルロケットが静止した状態から飛び出す状況を考える。時刻t<0では、図2(a)と同じ状態であり、t=0にストッパーを外して動けるようになったとする(図3(a))。t=△tでは、水を噴出したロケットは上向きに動いている(図3(b))。t=0での、ペットボトルと内部の水やノズルを含むロケット全体の質量をM、速さを0とする。また、t=△tでの、ロケット全体の質量をM′、速さを△v、△tの間に噴出した水の速さをu′とする。△tが小さいときには、△mと△vも小さいので、M′をMに、u′をuに等しいとみなせるものとする。ペットボトル内部の水の流れの影響は考えなくてよいものとする。
時刻t=△tでのロケットの運動量と噴出した水の運動量の和は、t=0でのロケットの運動量に等しいと考えられる。その関係を表す式として最も適当なものを、次の選択肢のうちから一つ選べ。

- △m△v+Mu=0
- △m△v-Mu=0
- M△v+△mu=0
- M△v-△mu=0
- (1/2)M(△v)2+(1/2)△mu2=0
- (1/2)M(△v)2−(1/2)△mu2=0
- (1/2)△m(△v)2+(1/2)Mu2=0
- (1/2)△m(△v)2−(1/2)Mu2=0
正解!素晴らしいです
残念...

この過去問の解説
前の問題(問73)へ
令和6年度(2024年度)本試験 問題一覧
次の問題(問75)へ