大学入学共通テスト(理科) 過去問
令和4年度(2022年度)本試験
問68 (物理(第1問) 問3)
問題文
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(理科)試験 令和4年度(2022年度)本試験 問68(物理(第1問) 問3) (訂正依頼・報告はこちら)

正解!素晴らしいです
残念...
MENU
あ
か
さ
た
な
は
ま
や
ら
あん摩マッサージ指圧師
1級管工事施工管理技士
1級建築施工管理技士
1級電気工事施工管理技士
1級土木施工管理技士
運行管理者(貨物)
2級ファイナンシャル・プランニング技能士(FP2級)
3級ファイナンシャル・プランニング技能士(FP3級)
貸金業務取扱主任者
危険物取扱者(乙4)
給水装置工事主任技術者
クレーン・デリック運転士
ケアマネジャー(介護支援専門員)
国内旅行業務取扱管理者
社会保険労務士(社労士)
大学入学共通テスト(国語)
大学入学共通テスト(地理歴史)
大学入学共通テスト(公民)
大学入学共通テスト(数学)
大学入学共通テスト(理科)
大学入学共通テスト(情報)
大学入学共通テスト(英語)
第三種電気主任技術者(電験三種)
宅地建物取引士(宅建士)
調剤報酬請求事務技能認定
賃貸不動産経営管理士
2級管工事施工管理技士
2級建築施工管理技士
2級電気工事施工管理技士
2級土木施工管理技士
JLPT(日本語能力)
建築物環境衛生管理技術者(ビル管理士)
問題文

このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
大学入学共通テスト(理科)試験 令和4年度(2022年度)本試験 問68(物理(第1問) 問3) (訂正依頼・報告はこちら)

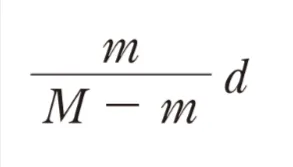
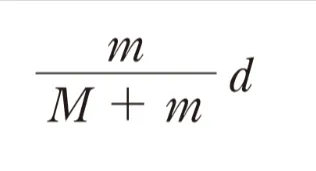
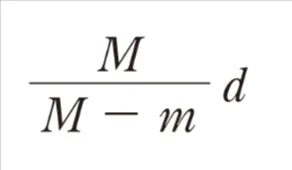
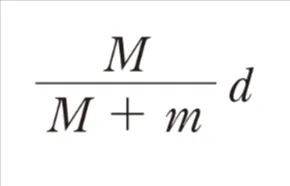
正解!素晴らしいです
残念...
この過去問の解説 (2件)
01
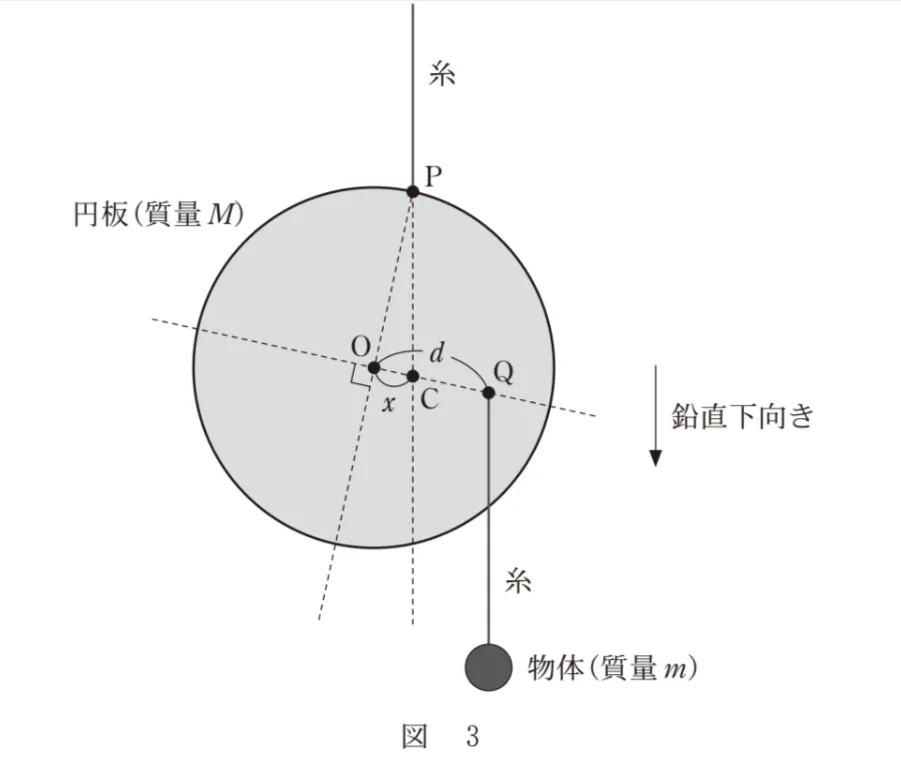
点線PCが糸の直線状にあることから、Cが重心であることが分かります。
つまり、次の式が成り立ちます。
x:d-x=m:M
それぞれの内積、外積を計算すると、
m(d-x)=Mx
md-mx=Mx
(m+M)x=md
∴x=md(m+M) となります。
これが正解です。
参考になった数0
この解説の修正を提案する
02
解答 {m/(M+m)}d
解説
点Pにかかる糸の張力によるモーメントは
Cのまわりを考えると0になることを活用します。
解法1(機械的に計算する方法)
Cのまわりの力のモーメントの釣り合いより(反時計回りを正)、
0 = Mgcos(∠OPC)・x - mgcos(∠OPC)・(d-x)
0 = Mx - m(d-x)
Mx = m(d-x)
Mx = md-mx
(M+m)x = d
x = {m/(M+m)}d
よって答えは {m/(M+m)}d となります。
解法2(推奨: 慣れると楽な方法)
点Cのまわりの力のモーメントの釣り合いに関して比で考える。
腕の長さの比は力の逆比になるので、
OC:CQ = (Qにかかる力のOPに平行な成分):(Oにかかる力のOPに平行な成分)
OC:CQ = (Qにかかる力):(Oにかかる力)
x:(d-x) = mg:Mg
x:(d-x) = m:M ←慣れたらいきなりこの式を書ける
Mx = m(d-x)
これをxについて解いて答えは {m/(M+m)}d となります。
解法3(重心の定義を使う解法)
点Oに質量M, 点Qに質量mの物体があって、
その重心がCになっていると考えることができます。
重心の定義式より
x = (M×0 + m×d)/(M+m)
式を整理して答えは {m/(M+m)}d となります。
この選択肢が正解となります。
力のモーメントの釣り合いや重心の定義について復習しておきましょう。
参考になった数0
この解説の修正を提案する
前の問題(問67)へ
令和4年度(2022年度)本試験 問題一覧
次の問題(問69)へ