大学入学共通テスト（理科） 過去問
令和4年度（2022年度）本試験
問86 (物理（第4問） 問1)
問題文
次の文章を読み、後の問いに答えよ。
水素原子を、図1のように、静止した正の電気量eを持つ陽子と、そのまわりを負の電気量－eを持つ電子が速さv、軌道半径rで等速円運動するモデルで考える。陽子および電子の大きさは無視できるものとする。陽子の質量をM，電子の質量をm，クーロンの法則の真空中での比例定数をk0，プランク定数をh，万有引力定数をG，真空中の光速をcとし、必要ならば、表1の物理定数を用いよ。
表1 物理定数
万有引力定数 （ G ） ［6.7✕10－11N・m2／kg2］
プランク定数 （ h ） ［6.6✕10－34J・s］
クーロンの法則の真空中での比例定数 （ k0 ） ［9.0✕109N・m2／C2］
真空中の光速 （ c ） ［3.0✕108m／s］
電気素量 （ e ） ［1.6✕10－19C］
陽子の質量 （ M ） ［1.7✕10－27kg］
電子の質量 （ m ） ［9.1✕10－31kg］
次の画像文章中の空欄ア・イに入れる式の組合せとして最も適当なものを、後の選択肢のうちから一つ選べ。
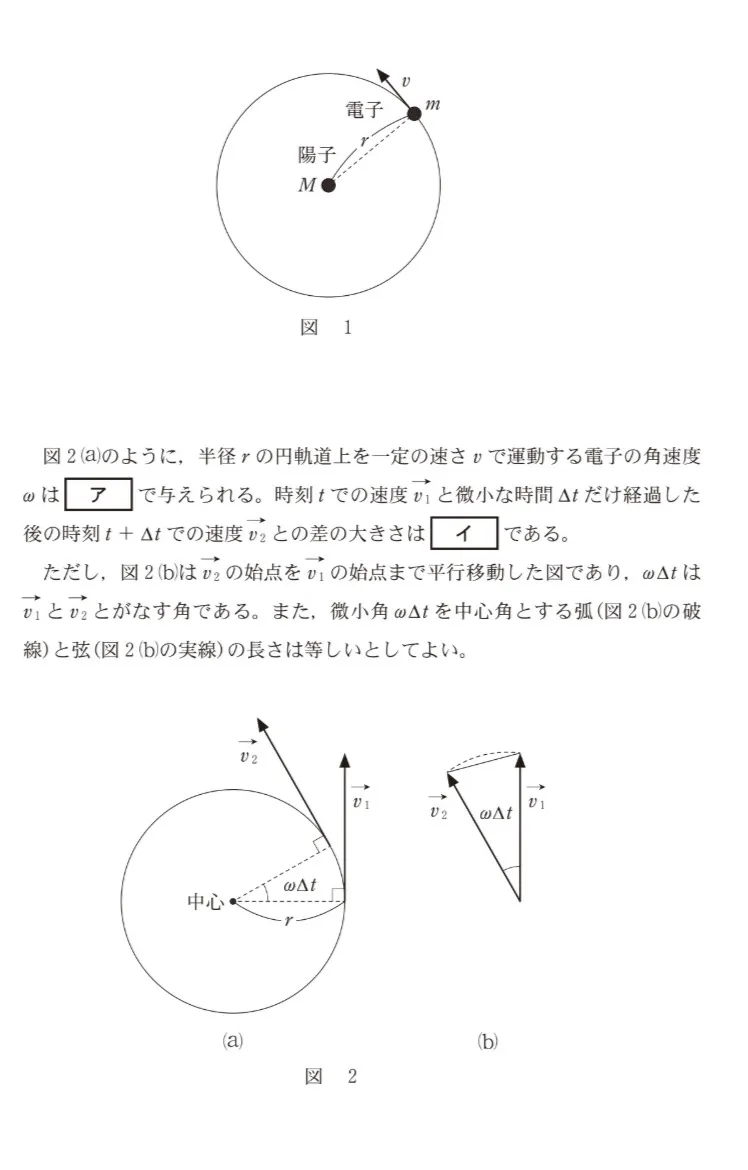
水素原子を、図1のように、静止した正の電気量eを持つ陽子と、そのまわりを負の電気量－eを持つ電子が速さv、軌道半径rで等速円運動するモデルで考える。陽子および電子の大きさは無視できるものとする。陽子の質量をM，電子の質量をm，クーロンの法則の真空中での比例定数をk0，プランク定数をh，万有引力定数をG，真空中の光速をcとし、必要ならば、表1の物理定数を用いよ。
表1 物理定数
万有引力定数 （ G ） ［6.7✕10－11N・m2／kg2］
プランク定数 （ h ） ［6.6✕10－34J・s］
クーロンの法則の真空中での比例定数 （ k0 ） ［9.0✕109N・m2／C2］
真空中の光速 （ c ） ［3.0✕108m／s］
電気素量 （ e ） ［1.6✕10－19C］
陽子の質量 （ M ） ［1.7✕10－27kg］
電子の質量 （ m ） ［9.1✕10－31kg］
次の画像文章中の空欄ア・イに入れる式の組合せとして最も適当なものを、後の選択肢のうちから一つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（理科）試験 令和4年度（2022年度）本試験 問86（物理（第4問） 問1） （訂正依頼・報告はこちら）
次の文章を読み、後の問いに答えよ。
水素原子を、図1のように、静止した正の電気量eを持つ陽子と、そのまわりを負の電気量－eを持つ電子が速さv、軌道半径rで等速円運動するモデルで考える。陽子および電子の大きさは無視できるものとする。陽子の質量をM，電子の質量をm，クーロンの法則の真空中での比例定数をk0，プランク定数をh，万有引力定数をG，真空中の光速をcとし、必要ならば、表1の物理定数を用いよ。
表1 物理定数
万有引力定数 （ G ） ［6.7✕10－11N・m2／kg2］
プランク定数 （ h ） ［6.6✕10－34J・s］
クーロンの法則の真空中での比例定数 （ k0 ） ［9.0✕109N・m2／C2］
真空中の光速 （ c ） ［3.0✕108m／s］
電気素量 （ e ） ［1.6✕10－19C］
陽子の質量 （ M ） ［1.7✕10－27kg］
電子の質量 （ m ） ［9.1✕10－31kg］
次の画像文章中の空欄ア・イに入れる式の組合せとして最も適当なものを、後の選択肢のうちから一つ選べ。
水素原子を、図1のように、静止した正の電気量eを持つ陽子と、そのまわりを負の電気量－eを持つ電子が速さv、軌道半径rで等速円運動するモデルで考える。陽子および電子の大きさは無視できるものとする。陽子の質量をM，電子の質量をm，クーロンの法則の真空中での比例定数をk0，プランク定数をh，万有引力定数をG，真空中の光速をcとし、必要ならば、表1の物理定数を用いよ。
表1 物理定数
万有引力定数 （ G ） ［6.7✕10－11N・m2／kg2］
プランク定数 （ h ） ［6.6✕10－34J・s］
クーロンの法則の真空中での比例定数 （ k0 ） ［9.0✕109N・m2／C2］
真空中の光速 （ c ） ［3.0✕108m／s］
電気素量 （ e ） ［1.6✕10－19C］
陽子の質量 （ M ） ［1.7✕10－27kg］
電子の質量 （ m ） ［9.1✕10－31kg］
次の画像文章中の空欄ア・イに入れる式の組合せとして最も適当なものを、後の選択肢のうちから一つ選べ。
- ア：rv イ：0
- ア：rv イ：rv2Δt
- ア：rv イ：（v2／r）Δt
- ア：v／r イ：0
- ア：v／r イ：rv2Δt
- ア：v／r イ：（v2／r）Δt
正解！素晴らしいです
残念...
この過去問の解説 （1件）
01
解答 ア：v／r イ：（v2／r）Δt
解説
速さv、半径rの等速円運動の角速度ωを求めます。
例えば、
(１周の角度2πを角速度ωで回る所要時間)
=(１周の長さ2πrを速さvで回る所要時間)
と考えて、
2π/ω = 2πr/v
両辺を2πで割って逆数を考えると
ω = v/r …① ←アの答え
となります。この①については公式として覚えておくべきです。
いま等速円運動を考えているので、
与えられた図中のv1,v2の大きさについて
v=|v1→|=|v2→| (表記注: 「→」はベクトルの意味)
です。
2つのベクトル(v2→)と(v1→)の差の大きさを
問題文に従って近似して計算します。
|(v2→)-(v1→)|
≒|(半径vで中心角ωΔtの扇形の孤の長さ)|
=vωΔt
=(v2/r)Δt (①を代入)
よって答えは ア：v／r イ：（v2／r）Δt となります。
なお、イの答えをΔtで割ると加速度の大きさ a=v2/r を得ます。
誤答選択肢です。
単位に着目することでこの選択肢と正解の選択肢の2択に
絞ることができ、図よりイの答えが0ではないことがすぐわかるため、
全く計算せずに正解の選択肢を選ぶことができます。
この選択肢が正解となります。
【円運動について】
円運動(等速に限らない)について、
半径:r (一定)、 速さ: v(一定でなくてよい) とすると、
角速度: ω=v/r (v=rω)
加速度の向心成分の大きさ: a⊥= v2／r = rω2
であり、
加速度の接線成分については
・等速円運動ではゼロ
・等速でない円運動ではゼロでない(数式は共通テスト範囲外)
とまとめられる。特に、
等速円運動の加速度の向き及び力の向きは常に中心方向である
ということは重要。
(加速度と力の向きが一致することは運動方程式からわかる)
【扇形について】
扇形の中心角の大きさが単位をラジアンとしてわかっているとき、
弧の長さ＝半径×中心角
参考になった数0
この解説の修正を提案する
前の問題（問85）へ
令和4年度（2022年度）本試験 問題一覧
次の問題（問87）へ