大学入学共通テスト(理科) 過去問
令和4年度(2022年度)本試験
問88 (物理(第4問) 問3)
問題文
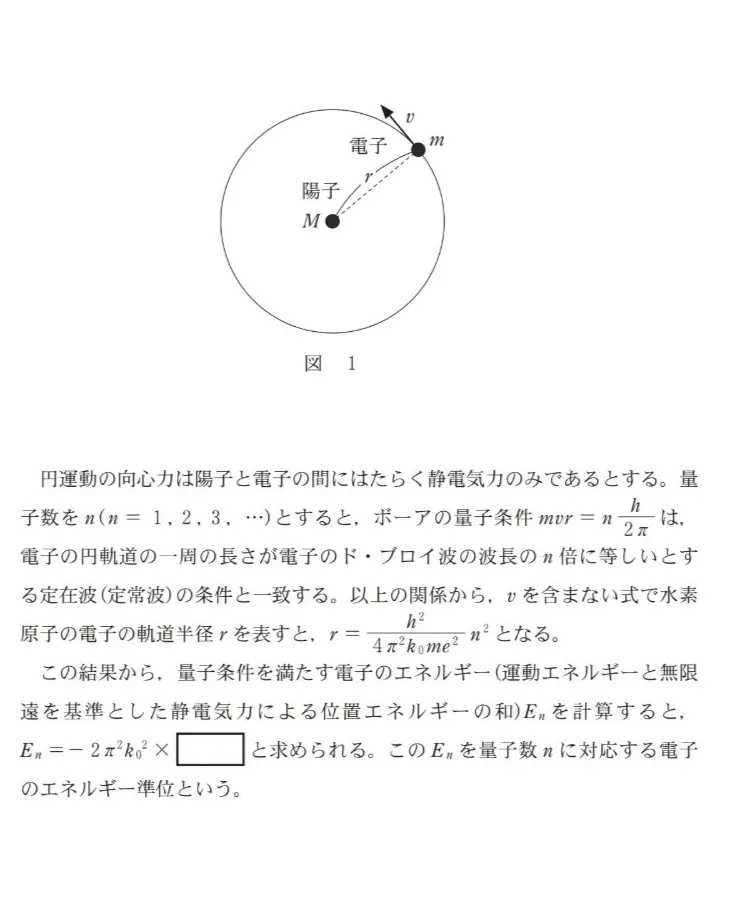
水素原子を、図1のように、静止した正の電気量eを持つ陽子と、そのまわりを負の電気量-eを持つ電子が速さv、軌道半径rで等速円運動するモデルで考える。陽子および電子の大きさは無視できるものとする。陽子の質量をM,電子の質量をm,クーロンの法則の真空中での比例定数をk0,プランク定数をh,万有引力定数をG,真空中の光速をcとし、必要ならば、表1の物理定数を用いよ。
表1 物理定数
万有引力定数 ( G ) [6.7✕10-11N・m2/kg2]
プランク定数 ( h ) [6.6✕10-34J・s]
クーロンの法則の真空中での比例定数 ( k0 ) [9.0✕109N・m2/C2]
真空中の光速 ( c ) [3.0✕108m/s]
電気素量 ( e ) [1.6✕10-19C]
陽子の質量 ( M ) [1.7✕10-27kg]
電子の質量 ( m ) [9.1✕10-31kg]
次の画像文章中の空欄( )に入れる式として正しいものを、後の選択肢のうちから一つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(理科)試験 令和4年度(2022年度)本試験 問88(物理(第4問) 問3) (訂正依頼・報告はこちら)
水素原子を、図1のように、静止した正の電気量eを持つ陽子と、そのまわりを負の電気量-eを持つ電子が速さv、軌道半径rで等速円運動するモデルで考える。陽子および電子の大きさは無視できるものとする。陽子の質量をM,電子の質量をm,クーロンの法則の真空中での比例定数をk0,プランク定数をh,万有引力定数をG,真空中の光速をcとし、必要ならば、表1の物理定数を用いよ。
表1 物理定数
万有引力定数 ( G ) [6.7✕10-11N・m2/kg2]
プランク定数 ( h ) [6.6✕10-34J・s]
クーロンの法則の真空中での比例定数 ( k0 ) [9.0✕109N・m2/C2]
真空中の光速 ( c ) [3.0✕108m/s]
電気素量 ( e ) [1.6✕10-19C]
陽子の質量 ( M ) [1.7✕10-27kg]
電子の質量 ( m ) [9.1✕10-31kg]
次の画像文章中の空欄( )に入れる式として正しいものを、後の選択肢のうちから一つ選べ。

正解!素晴らしいです
残念...

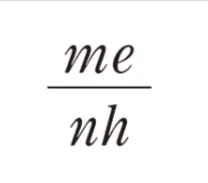
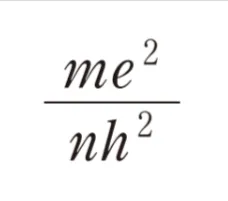
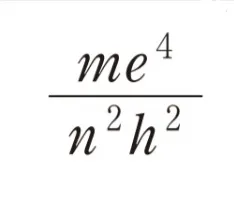
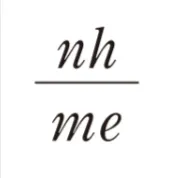
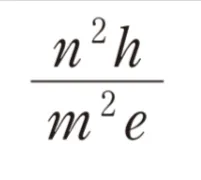
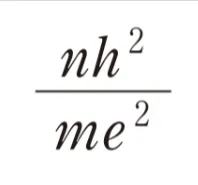
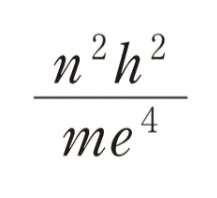
この過去問の解説 (2件)
01
問題文に求めたいEnは「電子の運動エネルギー」と、「無限遠を基準とした静電気力による位置エネルギー」の和であることが記されているためそれぞれを求めてきましょう。
まず電子の運動エネルギーは1/2mv2ですが今回vは使えません。そこで
円運動の向心力の式mv2/r=k0e2/r2を使ってvを既知の別の値に書き換えると、
1/2mv2=k0e2/2rと表すことができます。
また、無限遠を基準とした静電気力による位置エネルギーは-k0e2/rなのでこれらを足し合わせると
En=k0e2/2r-k0e2/r=-k0e2/2r
これに与えられたrの値を代入すれば-2π2k02×me4/n2h2 となります。
これが正解です。
参考になった数0
この解説の修正を提案する
02
解答 me4/(n2h2)
解説
直前の問題より重力は無視して考えます。
この問題は文字が多いですが、
そのうち未知量はv, r, Eの3つです。
よって式が3つ必要になり、それは以下の3式です。
①ボーアの量子条件
mvr = nh/(2π) 変形して v=nh/(2πmr) …①
②電子の運動方程式
m(v2/r)=k0(e2/r2) 変形して mv2=k0(e2/r) …②
③電子のエネルギー
E = (1/2)mv2 - k0(e2/r) …③
v, r, EのうちEを求めたいので、vとrを消すことを考えます。
先にvを消し、後でrを消しましょう。
(手順1)まず①と②を合わせてvを消します。
この結果は問題文で与えられており、
r = (n2h2)/(4π2k0me2) …④
となります(実際に①を②に代入して確かめてみましょう)。
(手順2)次に②と③を合わせてvを消します。
②を③に代入して
E = -(1/2)k0(e2/r) …⑤
(手順3)最後に④と⑤を合わせてrを消します。
④より
1/r = (4π2k0me2)/(n2h2)
であるから、
E = -(1/2)k0e2×(4π2k0me2)/(n2h2)
= -2π2k02×{(me4)/(n2h2)}
最後にEがnに依存することを明示して(EをEnに書き換えて)
En = -2π2k02×{(me4)/(n2h2)}
となります。
よって答えは me4/(n2h2) となります。
この選択肢が正解となります。
なお、
・エネルギーはその単位からして E=(単位のない定数)×(k0e2/r) の形で書けるはず
・問題文より 1/r =(単位のない定数)×(k0me2)/(n2h2) である
ということから
E=(単位のない定数)×(k02me4)/(n2h2)
と考えると素早く判断できます。
水素原子中の電子のエネルギー準位Enを求める問題は、
共通テスト・2次試験ともに頻出です。解き方の流れを覚えておきましょう。
エネルギー準位の求め方
未知量はv, r, Eの3つ→式が3つ必要
①ボーアの量子条件 ②電子の運動方程式 ③電子のエネルギー
(手順1)①と②からvを消した式を④とする
(手順2)②と③からvを消した式を⑤とする
(手順3)④と⑤からrを消す
なお、出題形式によっては最初に
ドブロイ波長: λ=h/(mv)
定在波の条件: 2πr = nλ
の2式からλを消して①を得る必要があります。
参考になった数0
この解説の修正を提案する
前の問題(問87)へ
令和4年度(2022年度)本試験 問題一覧
次の問題(問89)へ