大学入学共通テスト（理科） 過去問
令和4年度（2022年度）追・再試験
問74 (物理（第1問） 問3)
問題文
次の問いに答えよ。
図5のように、長さがLで太さが一様な抵抗線ab，抵抗値がR1の抵抗、抵抗値がR2の抵抗、検流計G、直流電源、電流計を接続する。接点cは、ab上を自由に移動できる。ここで、点cをab上で動かし、検流計Gに電流が流れない点を見つけた。このときのac間の距離をxとした場合、R1／R2を表す式として正しいものを、後の選択肢のうちから一つ選べ。
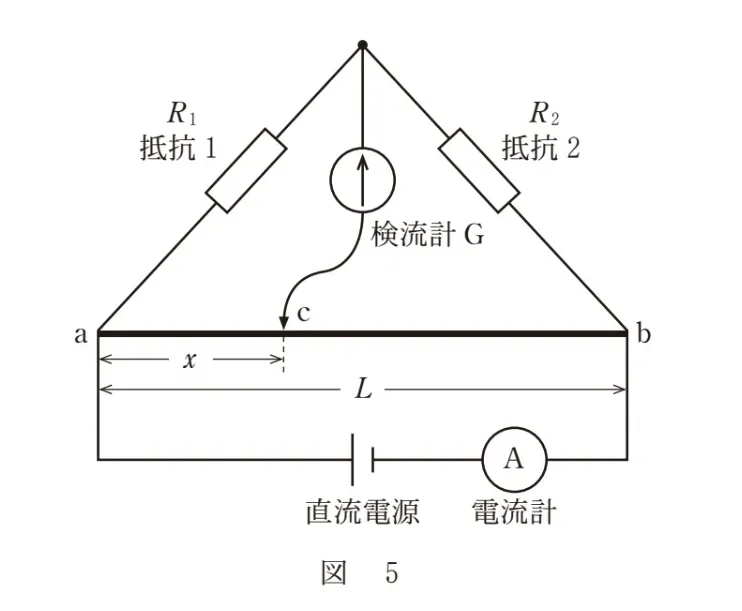
図5のように、長さがLで太さが一様な抵抗線ab，抵抗値がR1の抵抗、抵抗値がR2の抵抗、検流計G、直流電源、電流計を接続する。接点cは、ab上を自由に移動できる。ここで、点cをab上で動かし、検流計Gに電流が流れない点を見つけた。このときのac間の距離をxとした場合、R1／R2を表す式として正しいものを、後の選択肢のうちから一つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（理科）試験 令和4年度（2022年度）追・再試験 問74（物理（第1問） 問3） （訂正依頼・報告はこちら）
次の問いに答えよ。
図5のように、長さがLで太さが一様な抵抗線ab，抵抗値がR1の抵抗、抵抗値がR2の抵抗、検流計G、直流電源、電流計を接続する。接点cは、ab上を自由に移動できる。ここで、点cをab上で動かし、検流計Gに電流が流れない点を見つけた。このときのac間の距離をxとした場合、R1／R2を表す式として正しいものを、後の選択肢のうちから一つ選べ。
図5のように、長さがLで太さが一様な抵抗線ab，抵抗値がR1の抵抗、抵抗値がR2の抵抗、検流計G、直流電源、電流計を接続する。接点cは、ab上を自由に移動できる。ここで、点cをab上で動かし、検流計Gに電流が流れない点を見つけた。このときのac間の距離をxとした場合、R1／R2を表す式として正しいものを、後の選択肢のうちから一つ選べ。
- x／L
- x／（L−x）
- x／（L＋x）
- L／x
- （L−X）／x
- （L＋X）／x
正解！素晴らしいです
残念...
この過去問の解説 （1件）
01
「検流計Gに電流が流れていない」ことからホイートストンブリッジの式を使うことが考えます。
長さがLで太さが一様な抵抗線abの抵抗をRとすると
acとcbの2つの直列の抵抗に分けて考え、
acの抵抗 (x/L)×R
cbの抵抗 ((L-x)/L)×R
となります。
ホイートストンブリッジの式より
R1×（cbの抵抗）＝R2×（acの抵抗）
より
R1×((L-x)/L)×R＝R2×(x/L)×R
R1×(L-x)＝R2×x
R1/R2＝x/(L-x)
が正答になります。
検流計に電流が流れていないときにはホイートストンブリッジの式を使えないか考えましょう。
また、一様な抵抗棒については直列で分けることができることがあるのでこれもポイントです。
参考になった数0
この解説の修正を提案する
前の問題（問73）へ
令和4年度（2022年度）追・再試験 問題一覧
次の問題（問75）へ