大学入学共通テスト(理科) 過去問
令和5年度(2023年度)本試験
問2 (物理基礎(第1問) 問2)
問題文
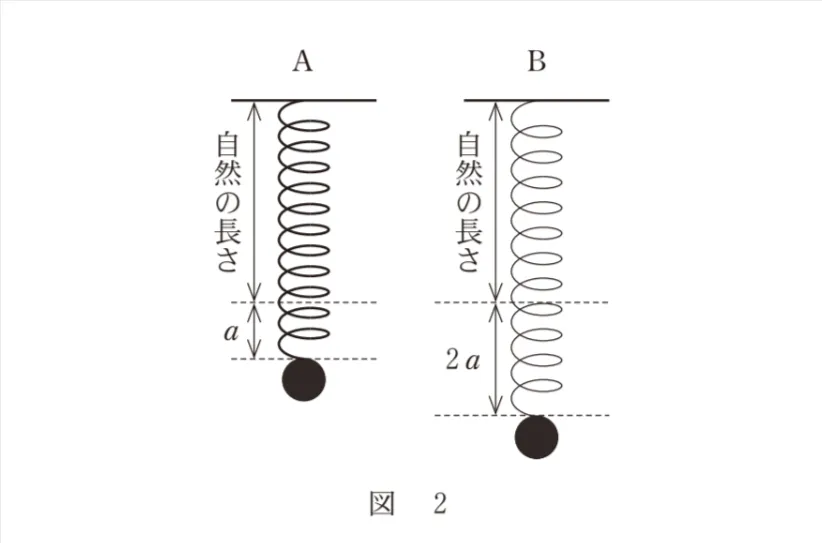
このとき、ばねBの弾性力による位置エネルギーは、ばねAの弾性力による位置エネルギーの何倍か。その値として最も適当なものを、次の選択肢のうちから一つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(理科)試験 令和5年度(2023年度)本試験 問2(物理基礎(第1問) 問2) (訂正依頼・報告はこちら)
このとき、ばねBの弾性力による位置エネルギーは、ばねAの弾性力による位置エネルギーの何倍か。その値として最も適当なものを、次の選択肢のうちから一つ選べ。

- 1/2
- √2/2
- 1
- √2
- 2
- 4
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
F=kx (F:力、k:ばね定数、x:伸び)でおもりの重さは同じのため
kA×a=kB×2a ∴kA=2kBとなります
また、ばねの弾性エネルギーは1/2kx2 (k:ばね定数, x:伸び)なので
ばねaの弾性エネルギーは1/2kAa2
ばねbの弾性エネルギーは1/2kB(2a)2=1/2×1/2kA×4a2=kAa2
よってばねBの弾性エネルギーはばねAの2倍となります。
これが正解です。
参考になった数0
この解説の修正を提案する
02
解答 2
解説
フックの法則と弾性エネルギーの公式の理解を問う問題です。
ばね定数をそれぞれkA,kBとおきます。
フックの法則に注意して力の釣り合い(鉛直上向きを正)より、
A: 0 = kA・a - mg
B: 0 = kB・2a - mg
2式から kB=(1/2)kA を得ます。
Bの弾性エネルギーがAの弾性エネルギーの何倍かを計算します。
(Bの弾性エネルギー)÷(Aの弾性エネルギー)
={(1/2)kB・(2a)2} ÷ (1/2)kAa2
={4・(1/2)kBa2} ÷ (1/2)kAa2
= 4kB/kA
= 2kA/kA (kB=(1/2)kAを代入)
=2
よって答えは 2 となります。
別解
ばね定数を先に消去する方針でも考えてみましょう。
フックの法則に注意して力の釣り合いより、
A: kAa = mg
B: kB・2a = mg
弾性エネルギーについて
A: (1/2)kA・a2 = (1/2)・kAa・a = (1/2)mga
B: (1/2)kB・(2a)2 = (1/2)・kB・(2a)・(2a) = mga
(Bの弾性エネルギー)÷(Aの弾性エネルギー)
=mga ÷ (1/2)mga
=2
よって答えは 2 となります。
この選択肢が正解となります。
公式を複数同時に使い、連立させるタイプの問題がある程度出題されます。
1つの公式だけで解決できると思い込まないようにしましょう。
また、与えられていない文字(今回ならばね定数)を自分で用意することも重要です。
参考になった数0
この解説の修正を提案する
前の問題(問1)へ
令和5年度(2023年度)本試験 問題一覧
次の問題(問3)へ