大学入学共通テスト(理科) 過去問
令和5年度(2023年度)本試験
問9 (物理基礎(第2問) 問4)
問題文
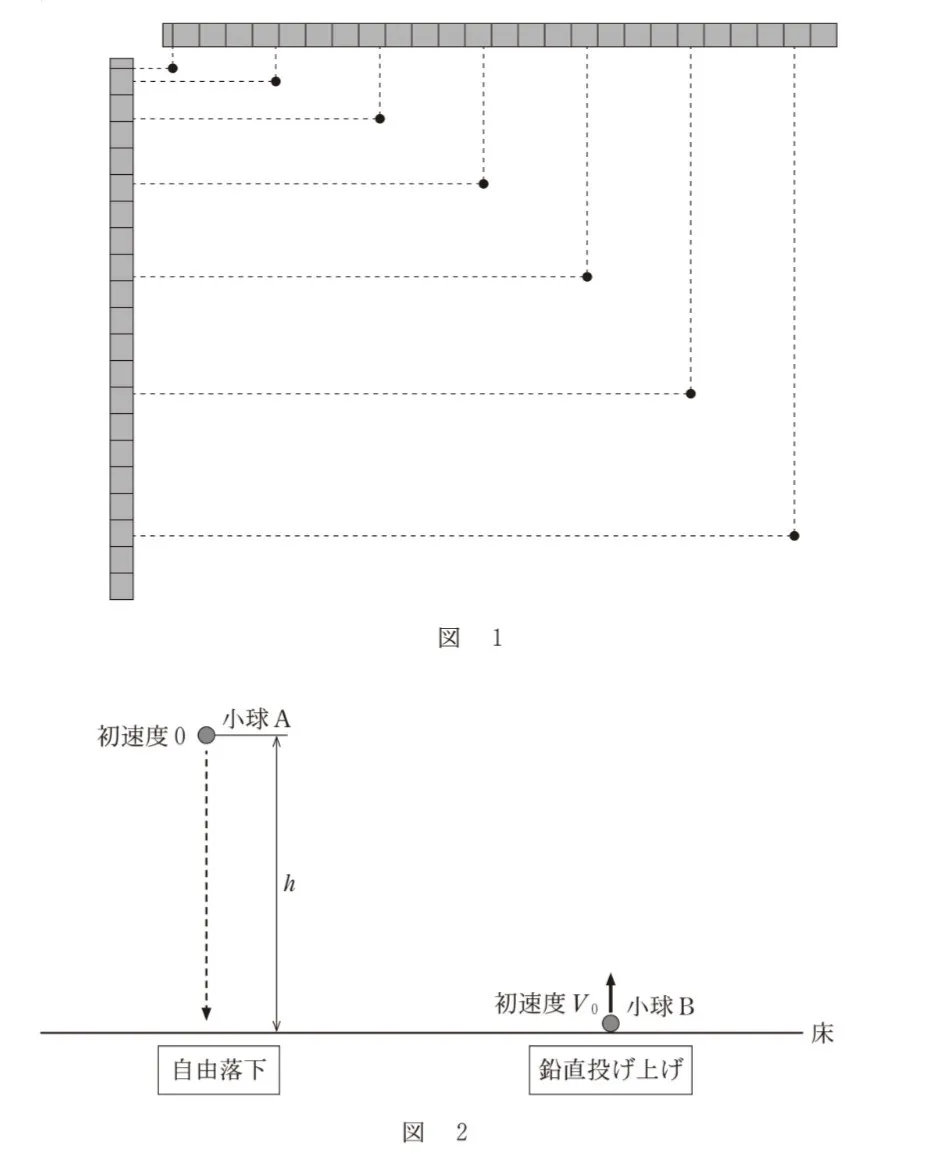
図1は、ある初速度で水平右向きに投射された小球を、0.1sの時間間隔で撮影した写真である。壁には目盛り間隔0.1mのものさしが水平な向きと鉛直な向きに固定されている。
同じ質量の二つの小球A、Bを用意した。図2のように、水平な床を高さの基準面として、小球Aを高さhの位置から初速度0で自由落下させると同時に、小球Bを床から初速度V0で鉛直に投げ上げたところ、小球A、Bは同時に床に到達した。
V0を、hと重力加速度の大きさgを用いて表す式として正しいものを、次の選択肢のうちから一つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(理科)試験 令和5年度(2023年度)本試験 問9(物理基礎(第2問) 問4) (訂正依頼・報告はこちら)
図1は、ある初速度で水平右向きに投射された小球を、0.1sの時間間隔で撮影した写真である。壁には目盛り間隔0.1mのものさしが水平な向きと鉛直な向きに固定されている。
同じ質量の二つの小球A、Bを用意した。図2のように、水平な床を高さの基準面として、小球Aを高さhの位置から初速度0で自由落下させると同時に、小球Bを床から初速度V0で鉛直に投げ上げたところ、小球A、Bは同時に床に到達した。
V0を、hと重力加速度の大きさgを用いて表す式として正しいものを、次の選択肢のうちから一つ選べ。

- √(h/g)
- √(g/h)
- √gh
- √(h/2g)
- √(g/2h)
- √(gh/2)
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
鉛直投げ上げによる高さxは下記の公式で表せます。
x=v0t-1/2gt2
床に落ちてきたときx=0なので、t=2v0/g となります。
また、自由落下による落下距離hは下記の公式で表せます。
h=1/2gt2
これにt=2v0/g を代入すると、
h=1/2g (2v0/g)2
h=2v02/g ∴v0=√gh/2 となります。
これが正解です。
参考になった数0
この解説の修正を提案する
02
解答 √(gh/2)
解説
等加速度直線運動の公式の理解度を問う問題です。
自由落下および鉛直投げ上げの問題であるため、
加速度aについて a=-g となります。
問題文中に「同時に床に到達」という「時刻に関する情報」が
あるため、時刻tを含む公式を使うことが分かります。
また、AもBも変位の情報は与えられている
(Aはhだけ下降し、Bの変位は0である)ので
x = v0t + (1/2)at2
の公式を使うとよいでしょう。
それぞれが床に到達する時刻をtA,tBとします。
A: -h = -(1/2)gtA2 より tA = √(2h/g)
B: 0 = V0tB-(1/2)gtB2 (tB≠0) より tB= 2V0/g
同時に床に到達するから
tB = tA
2V0/g = √(2h/g)
V0 = {√(2h/g)} ・(g/2)
V0 = √(gh/2)
(もしルートの計算が苦手な場合は、いったん
tB2 = tA2として考えるとよいでしょう)
よって答えは √(gh/2) となります。
補足
Bの方については対称性より
床に到達する瞬間の速度が-V0とわかるので、
-V0 = V0 - gtB
tB = 2V0/g …(※)
としてもよいでしょう。
別解(やや高度な解法)
自由落下する立場から見ると重力の影響が消えて見えるため、
AからBを見ると、
BがAに向かって速度V0で等速直線運動しているように見えます。
AとBの間隔ははじめはhであり、最終的に0になるため、
tA = tB = h/V0
となります。これと(※)より
2V0/g = h/V0
となり、式を整理して
V0=√(gh/2) を得ることができます。
誤答選択肢です。
そもそも単位が速さになっているのは
正解の選択肢とこの選択肢の2つのみであるため、
実質2択問題です。
この選択肢が正解となります。
等加速度直線運動の公式を使いこなせるようになっておきましょう。
なお、必須ではありませんが、
√{(加速度)×(長さ)} の単位 = 速さの単位
ということを覚えておくとより自信を持って解答できます。
これは
√(m/s2 ・ m) = √(m2/s2) =m/s
のように直接確認する方法のほか、
「mghと(1/2)mv2の単位が同じ(両方エネルギー)」
→「ghとv2の単位が同じ」
→「√ghとvの単位が同じ」
という手続きでも思い出せます。
参考になった数0
この解説の修正を提案する
前の問題(問8)へ
令和5年度(2023年度)本試験 問題一覧
次の問題(問10)へ