大学入学共通テスト(理科) 過去問
令和5年度(2023年度)本試験
問10 (物理基礎(第2問) 問5)
問題文
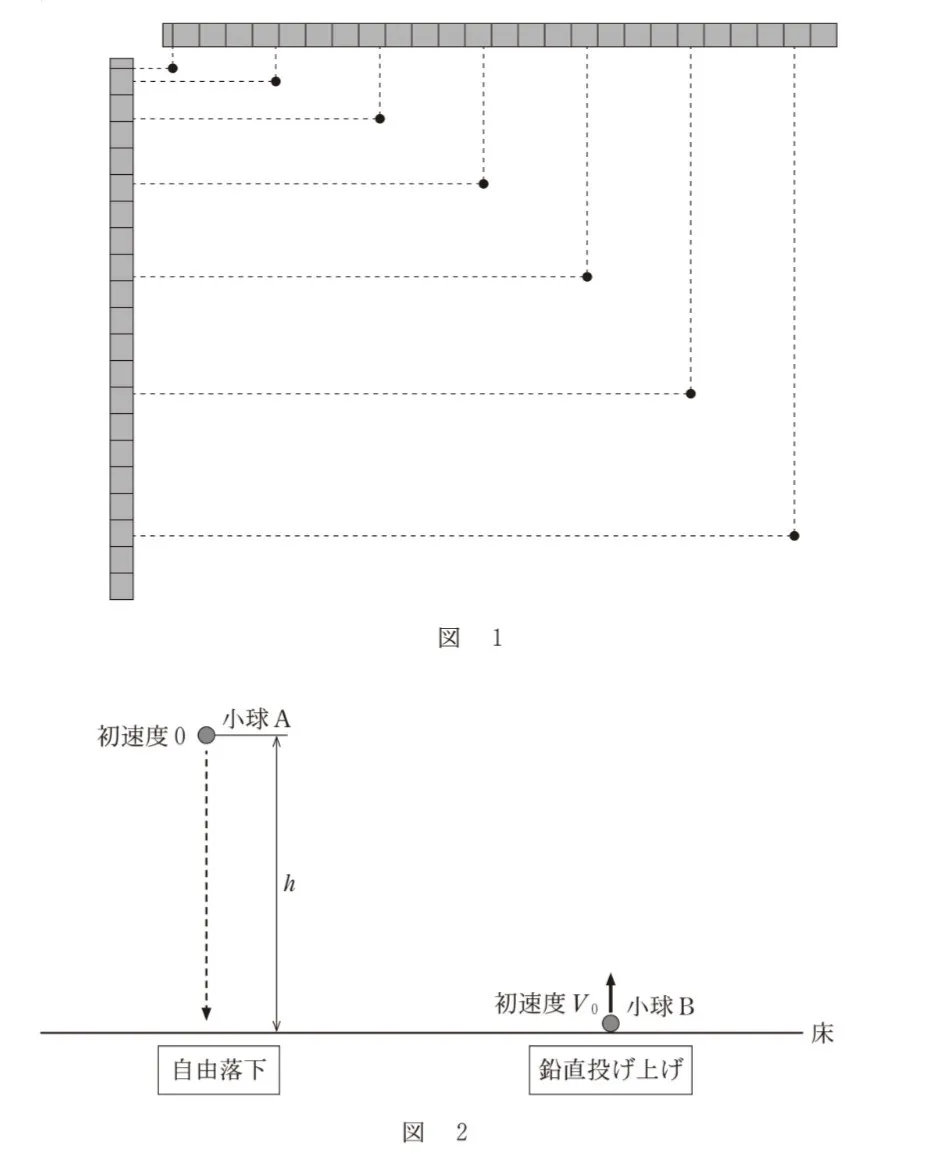
図1は、ある初速度で水平右向きに投射された小球を、0.1sの時間間隔で撮影した写真である。壁には目盛り間隔0.1mのものさしが水平な向きと鉛直な向きに固定されている。
同じ質量の二つの小球A、Bを用意した。図2のように、水平な床を高さの基準面として、小球Aを高さhの位置から初速度0で自由落下させると同時に、小球Bを床から初速度V0で鉛直に投げ上げたところ、小球A、Bは同時に床に到達した。
次の文章中の( ア )・( イ )に入れる式の組合せとして正しいものを、後の選択肢のうちから一つ選べ。
床に到達する時点での小球A、Bの運動エネルギーKA、KBの大小関係は、計算をせずとも以下のように調べられる。
小球Bの最高点の高さをhBとする。運動を開始してから床に到達するまでの時間は小球A、Bで等しいことから、hとhBの大小関係は( ア )であることがわかる。小球が最高点から床に達する間に失った重力による位置エネルギーは、床に到達する時点で運動エネルギーにすべて変換されるので、KAとKBの大小関係は( イ )であることがわかる。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(理科)試験 令和5年度(2023年度)本試験 問10(物理基礎(第2問) 問5) (訂正依頼・報告はこちら)
図1は、ある初速度で水平右向きに投射された小球を、0.1sの時間間隔で撮影した写真である。壁には目盛り間隔0.1mのものさしが水平な向きと鉛直な向きに固定されている。
同じ質量の二つの小球A、Bを用意した。図2のように、水平な床を高さの基準面として、小球Aを高さhの位置から初速度0で自由落下させると同時に、小球Bを床から初速度V0で鉛直に投げ上げたところ、小球A、Bは同時に床に到達した。
次の文章中の( ア )・( イ )に入れる式の組合せとして正しいものを、後の選択肢のうちから一つ選べ。
床に到達する時点での小球A、Bの運動エネルギーKA、KBの大小関係は、計算をせずとも以下のように調べられる。
小球Bの最高点の高さをhBとする。運動を開始してから床に到達するまでの時間は小球A、Bで等しいことから、hとhBの大小関係は( ア )であることがわかる。小球が最高点から床に達する間に失った重力による位置エネルギーは、床に到達する時点で運動エネルギーにすべて変換されるので、KAとKBの大小関係は( イ )であることがわかる。

- ア:h=hB イ:KA>KB
- ア:h=hB イ:KA<KB
- ア:h=hB イ:KA=KB
- ア:h<hB イ:KA>KB
- ア:h<hB イ:KA<KB
- ア:h<hB イ:KA=KB
- ア:h>hB イ:KA>KB
- ア:h>hB イ:KA<KB
- ア:h>hB イ:KA=KB
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
小球Bは高さhBまで上がったとき、運動エネルギーが0となりそのタイミングで自由落下し始めます。
一方で小球Aはt=0のときから自由落下しているため、自由落下している時間は小球Aの方が長くなります。
つまり高さh>hBとなります。
また、自由落下し始めるタイミングではどちらも運動エネルギーが0で位置エネルギーのみを持っているため、
高さが高い小球Aの方が床に到達する時点での運動エネルギーは大きくなります。
これが正解です。
参考になった数0
この解説の修正を提案する
02
解答 ア:h>hB イ:KA>KB
解説
床に到達する時点での小球A、Bの運動エネルギーKA、KBの
大小関係を問う問題です。
まず小球Bの最高点の高さhBとhの大小関係を考えます。
床に同時に到達することから、
(Aがhだけ落下するのにかかる時間)
=(Bが床から最高点まで到達するのにかかる時間)
+(Bが最高点から床まで到達するのにかかる時間)
であり、この式から当然
(Aがhだけ落下するのにかかる時間)>(Bが最高点から床まで到達するのにかかる時間)
となります。ということはBの最高点はhより低く、
h>hB ←アの答え
ということになります。
小球の質量をmとすると
小球が最高点から床に達する間に失った重力による位置エネルギーは
それぞれmgh, mghBと表せますが、その大小関係は
mgh>mghB
と分かり、これが全て運動エネルギーに変換されるため、
KA>KB ←イ:の答え
となります。
答えをまとめると ア:h>hB イ:KA>KB となります。
補足
問題文には「計算をせずとも」とありますが、
もしよくわからなくて手が止まってしまった場合は
計算したほうがよいでしょう。
最高点では一瞬小球が静止することに注意して、
力学的エネルギー保存の法則より、
mghB = (1/2)mV02
直前の問題の答えより V02 = gh/2 であり、これを代入して
mghB = (1/4)mgh
hB = (1/4)h
よって h>hB ←アの答え
となります。
この選択肢が正解となります。
参考になった数0
この解説の修正を提案する
前の問題(問9)へ
令和5年度(2023年度)本試験 問題一覧
次の問題(問11)へ