大学入学共通テスト(理科) 過去問
令和5年度(2023年度)追・再試験
問67 (物理(第1問) 問5)
問題文
次の文章中の空欄ケ~サに入れるものの組合せとして最も適当なものを、後の選択肢のうちから一つ選べ。
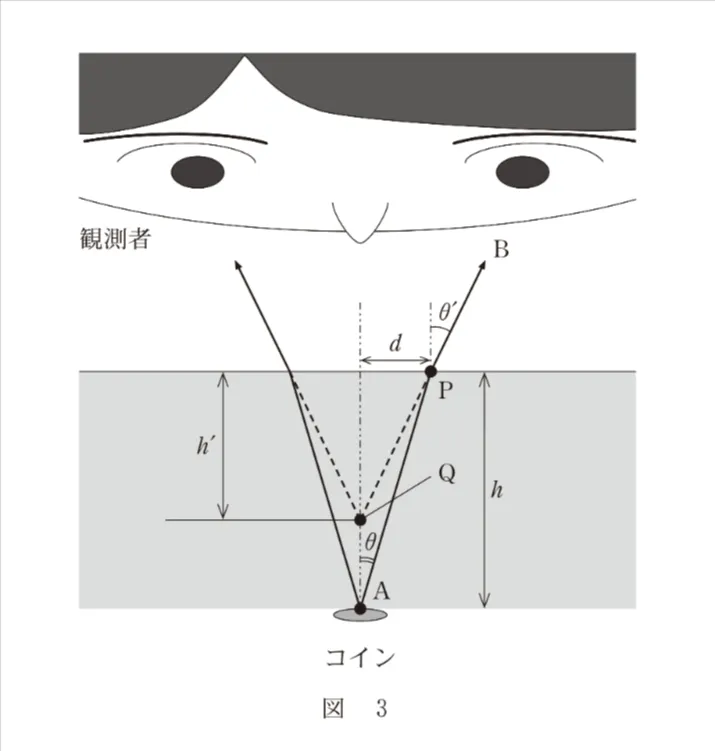
深さhの水の底に落ちているコインを真上から見る。ここではコインの見かけの深さを考察しよう。水の空気に対する屈折率をn(n>1)とする。図3のように、点Aから出て目に入る光は、鉛直線に対し角θの方向に進み、水面の点Pで鉛直線に対し角θ′の方向に屈折し、Bの方向に進んだ光である。点Aを通る鉛直線と点Pとの距離をd、直線BPが鉛直線と交わる点をQとする。角θ、θ′がきわめて小さいとして考えると、sinθ≒tanθ、sinθ′≒tanθ′と近似できるので、点Qの水面からの深さh′は、( ケ )と表される。このように、h′は( コ )によらず、点Aからθの小さい方向に進む光はどれも、( サ )から出ているように見え、コインの位置は実際より浅く見える。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(理科)試験 令和5年度(2023年度)追・再試験 問67(物理(第1問) 問5) (訂正依頼・報告はこちら)
次の文章中の空欄ケ~サに入れるものの組合せとして最も適当なものを、後の選択肢のうちから一つ選べ。
深さhの水の底に落ちているコインを真上から見る。ここではコインの見かけの深さを考察しよう。水の空気に対する屈折率をn(n>1)とする。図3のように、点Aから出て目に入る光は、鉛直線に対し角θの方向に進み、水面の点Pで鉛直線に対し角θ′の方向に屈折し、Bの方向に進んだ光である。点Aを通る鉛直線と点Pとの距離をd、直線BPが鉛直線と交わる点をQとする。角θ、θ′がきわめて小さいとして考えると、sinθ≒tanθ、sinθ′≒tanθ′と近似できるので、点Qの水面からの深さh′は、( ケ )と表される。このように、h′は( コ )によらず、点Aからθの小さい方向に進む光はどれも、( サ )から出ているように見え、コインの位置は実際より浅く見える。

- ケ:n/h コ:d サ:点P
- ケ:n/h コ:d サ:点Q
- ケ:h/n コ:d サ:点P
- ケ:h/n コ:d サ:点Q
- ケ:n/d コ:h サ:点P
- ケ:n/d コ:h サ:点Q
- ケ:d/n コ:h サ:点P
- ケ:d/n コ:h サ:点Q
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
屈折の法則(スネルの法則)を用いて考えます。
屈折の法則(スネルの法則)より、
液相と気相では、
n・sinθ=1・sinθ’
となります。
問題より、
sinθ=tanθ=d/h
sinθ'=tanθ'=d/h'
と近似できます。
屈折の法則(スネルの法則)に代入すると、
nd/h=d/h'
h'=h/n
となります。
このh'を構成する式にはdが含まれていないため、h'はdによらないといえます。
点Aからθの小さい方向に進む光はどれもQから出ているように見え、人間はQにコインがあるように錯覚します。
参考になった数0
この解説の修正を提案する
前の問題(問66)へ
令和5年度(2023年度)追・再試験 問題一覧
次の問題(問68)へ