大学入学共通テスト(理科) 過去問
令和5年度(2023年度)追・再試験
問81 (物理(第4問) 問5)
問題文
授業中の外部の騒音に困ったPさんとQさんは「音を使って音を消すことはできないのかな?」と考え、先生に相談した。次の問いに答えよ。ただし、会話文の内容は正しいものとする。
次の会話文の空欄( B )に入れる式として最も適当なものを、選択肢のうちから一つ選べ。
先生: 問3 で求めた図において合成波の変位が0の位置で、時間によらずその変位が0になるかどうかを数式で確認してみましょう。
図5がt=0の瞬間だと考えると、時刻tにおける波源Aから出た波(−−−−)の点Aでの変位も、波源Bから出た波(・・・・・・・)の点Bでの変位も、振幅をA0、周期をTとしてA0cos(2πt/T)という同じ式で表現されます。
Pさん:まず、点Bの右側(5λ/2≦x)を考えてみます。図5を見ると、ここでは二つの波の変位の向きが逆になっていて、波の進行方向が同じです。
Qさん:二つの波源の間の距離は5λ/2なので、点Bの右側では波源Aから出た波と波源Bから出た波の間には常に( A )の位相の差が生じます。
先生:点Bの右側では、二つの波は常に逆位相になっているので、打ち消しあうことが確認できました。この打ち消しあいは点Aの左側でも同じですね。
次に、点Aと点Bの間(0<x<5λ/2)の範囲を考えてみましょう。時刻t、座標xの点における波源Aから出た波の変位は、
yA=A0cos(2π/T){t-(x/v)}と表されます。
Qさん:波源Bから出た波も同様に考えることができます。点Bから座標xまでの距離を考えれば、時刻t、座標xの点における波源Bから出た波の変位は、
yB=( B )と表されます。
先生:波が打ち消しあう位置では、波源Aから出た波と波源Bから出た波の位相が常に逆になっています。合成波の変位yA+yBの式に、問3で求めた合成波の図において変位が0の座標xを代入すると、時間によらずその位置の変位が0となることが確認できるでしょう。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(理科)試験 令和5年度(2023年度)追・再試験 問81(物理(第4問) 問5) (訂正依頼・報告はこちら)
授業中の外部の騒音に困ったPさんとQさんは「音を使って音を消すことはできないのかな?」と考え、先生に相談した。次の問いに答えよ。ただし、会話文の内容は正しいものとする。
次の会話文の空欄( B )に入れる式として最も適当なものを、選択肢のうちから一つ選べ。
先生: 問3 で求めた図において合成波の変位が0の位置で、時間によらずその変位が0になるかどうかを数式で確認してみましょう。
図5がt=0の瞬間だと考えると、時刻tにおける波源Aから出た波(−−−−)の点Aでの変位も、波源Bから出た波(・・・・・・・)の点Bでの変位も、振幅をA0、周期をTとしてA0cos(2πt/T)という同じ式で表現されます。
Pさん:まず、点Bの右側(5λ/2≦x)を考えてみます。図5を見ると、ここでは二つの波の変位の向きが逆になっていて、波の進行方向が同じです。
Qさん:二つの波源の間の距離は5λ/2なので、点Bの右側では波源Aから出た波と波源Bから出た波の間には常に( A )の位相の差が生じます。
先生:点Bの右側では、二つの波は常に逆位相になっているので、打ち消しあうことが確認できました。この打ち消しあいは点Aの左側でも同じですね。
次に、点Aと点Bの間(0<x<5λ/2)の範囲を考えてみましょう。時刻t、座標xの点における波源Aから出た波の変位は、
yA=A0cos(2π/T){t-(x/v)}と表されます。
Qさん:波源Bから出た波も同様に考えることができます。点Bから座標xまでの距離を考えれば、時刻t、座標xの点における波源Bから出た波の変位は、
yB=( B )と表されます。
先生:波が打ち消しあう位置では、波源Aから出た波と波源Bから出た波の位相が常に逆になっています。合成波の変位yA+yBの式に、問3で求めた合成波の図において変位が0の座標xを代入すると、時間によらずその位置の変位が0となることが確認できるでしょう。
正解!素晴らしいです
残念...

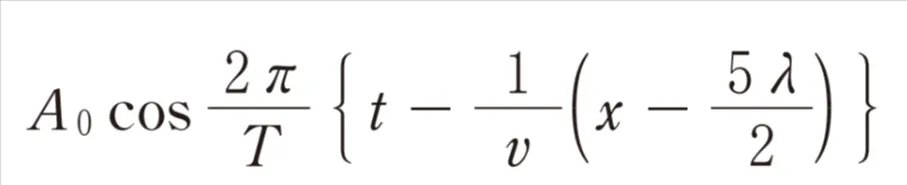
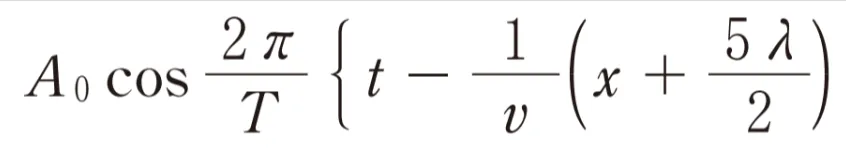
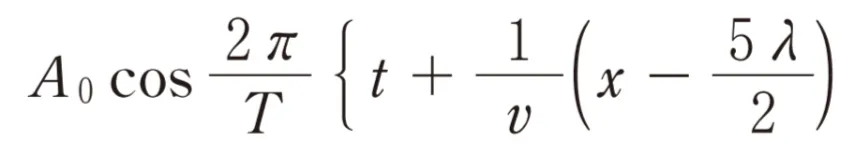
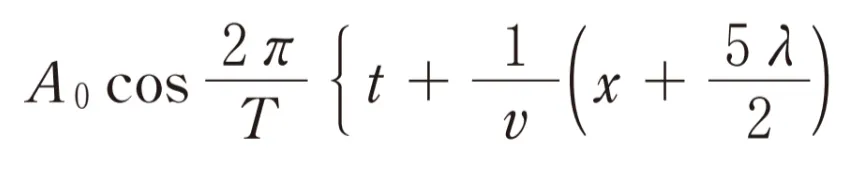
この過去問の解説 (1件)
01
波の変位を表す式を考える問題です。
Aと同様に、B(x=5λ/2)地点の波の変位を表す式は、A0cos(2πt/T)です。
次にx地点にBから発せられた波が到着する時間sを考えます。
xとB(x=5λ/2)の距離は、0<x<5λ/2なので、
5λ/2ーxで表されます。
この距離を速度vで移動するので、
s=(5λ/2ーx)/v
時間tのタイミングのx地点のBの波の変位は、時間sだけ前にBから発せられた波である為、
yB=A0cos(2π(tーs)/T)
=A0cos(2π(tー(5λ/2ーx)/v)/T)
=A0cos(2π(t+(x-5λ/2)/v)/T)
となります。
参考になった数0
この解説の修正を提案する
前の問題(問80)へ
令和5年度(2023年度)追・再試験 問題一覧
次の問題(問82)へ