大学入学共通テスト（理科） 過去問
令和5年度（2023年度）追・再試験
問112 (化学（第5問） 問7)
問題文
次の文章を読み、後の問いに答えよ。
（a）モノマー間の共有結合だけで網目状の立体構造をつくっている高分子や、架橋構造（橋かけ構造）により網目状の立体構造をつくっている高分子は、機能性高分子などとして身のまわりで多く利用されている。（b）ポリアクリル酸ナトリウムに架橋構造をもたせ、網目状の立体構造となった高分子は、高吸水性樹脂（吸水性高分子）として利用されている。この高吸水性樹脂内部には電離する官能基―COONaが存在する。（c）高吸水性樹脂を水に浸すと、水分子が樹脂の中に吸収され、樹脂の内側と外側でイオン濃度が異なるため浸透圧が生じる。すると水分子がさらに吸収され、網目が広がって図1のように樹脂が膨らむが、分子鎖が共有結合で架橋されているため、樹脂内に一定量の水が保持された状態で吸水がとまる。浸透圧については、希薄溶液では一般にファントホッフの法則が成り立つ。（d）ファントホッフの法則を用いると、浸透圧や溶質の分子量を決定することができる。
下線部（d）に関する次の問いに答えよ。
高分子の溶液では、式（1）は質量濃度CWが小さいときにしか適用できないが、次の式（2）はCWが大きくても適用できる。
Π＝CWRT｛（1／M′）＋ACW｝ （2）
ここで、M′は非電解質の高分子の平均分子量であり、Aは高分子間および高分子と溶媒との間の相互作用の大きさに関係する定数である。
式（2）を変形すると次の式（3）になり、M′を求めることができる。
Π／CWRT＝（1／M′）＋ACW （3）
CWが0に近づくとΠもCWRTも0に近づくが、式（3）が示すように、その比Π／CWRTは1／M′に近づくことを利用する。具体的には、CWが異なるいくつかの試料を調製し、それぞれに対してΠを測定する。得られた結果を用いてCWを横軸に、Π／CWRTを縦軸にとってグラフに表すと、CW＝0での切片からM′を求めることができる。
300Kで、ある非電解質の高分子の質量濃度CWを変化させてΠを測定し、Π／CWRTを求めると表1のようになった。表1の値を方眼紙に記入すると、図2のようになる。この高分子のM′はいくらか。最も適当な数値を、後の選択肢のうちから一つ選べ。
（a）モノマー間の共有結合だけで網目状の立体構造をつくっている高分子や、架橋構造（橋かけ構造）により網目状の立体構造をつくっている高分子は、機能性高分子などとして身のまわりで多く利用されている。（b）ポリアクリル酸ナトリウムに架橋構造をもたせ、網目状の立体構造となった高分子は、高吸水性樹脂（吸水性高分子）として利用されている。この高吸水性樹脂内部には電離する官能基―COONaが存在する。（c）高吸水性樹脂を水に浸すと、水分子が樹脂の中に吸収され、樹脂の内側と外側でイオン濃度が異なるため浸透圧が生じる。すると水分子がさらに吸収され、網目が広がって図1のように樹脂が膨らむが、分子鎖が共有結合で架橋されているため、樹脂内に一定量の水が保持された状態で吸水がとまる。浸透圧については、希薄溶液では一般にファントホッフの法則が成り立つ。（d）ファントホッフの法則を用いると、浸透圧や溶質の分子量を決定することができる。
下線部（d）に関する次の問いに答えよ。
高分子の溶液では、式（1）は質量濃度CWが小さいときにしか適用できないが、次の式（2）はCWが大きくても適用できる。
Π＝CWRT｛（1／M′）＋ACW｝ （2）
ここで、M′は非電解質の高分子の平均分子量であり、Aは高分子間および高分子と溶媒との間の相互作用の大きさに関係する定数である。
式（2）を変形すると次の式（3）になり、M′を求めることができる。
Π／CWRT＝（1／M′）＋ACW （3）
CWが0に近づくとΠもCWRTも0に近づくが、式（3）が示すように、その比Π／CWRTは1／M′に近づくことを利用する。具体的には、CWが異なるいくつかの試料を調製し、それぞれに対してΠを測定する。得られた結果を用いてCWを横軸に、Π／CWRTを縦軸にとってグラフに表すと、CW＝0での切片からM′を求めることができる。
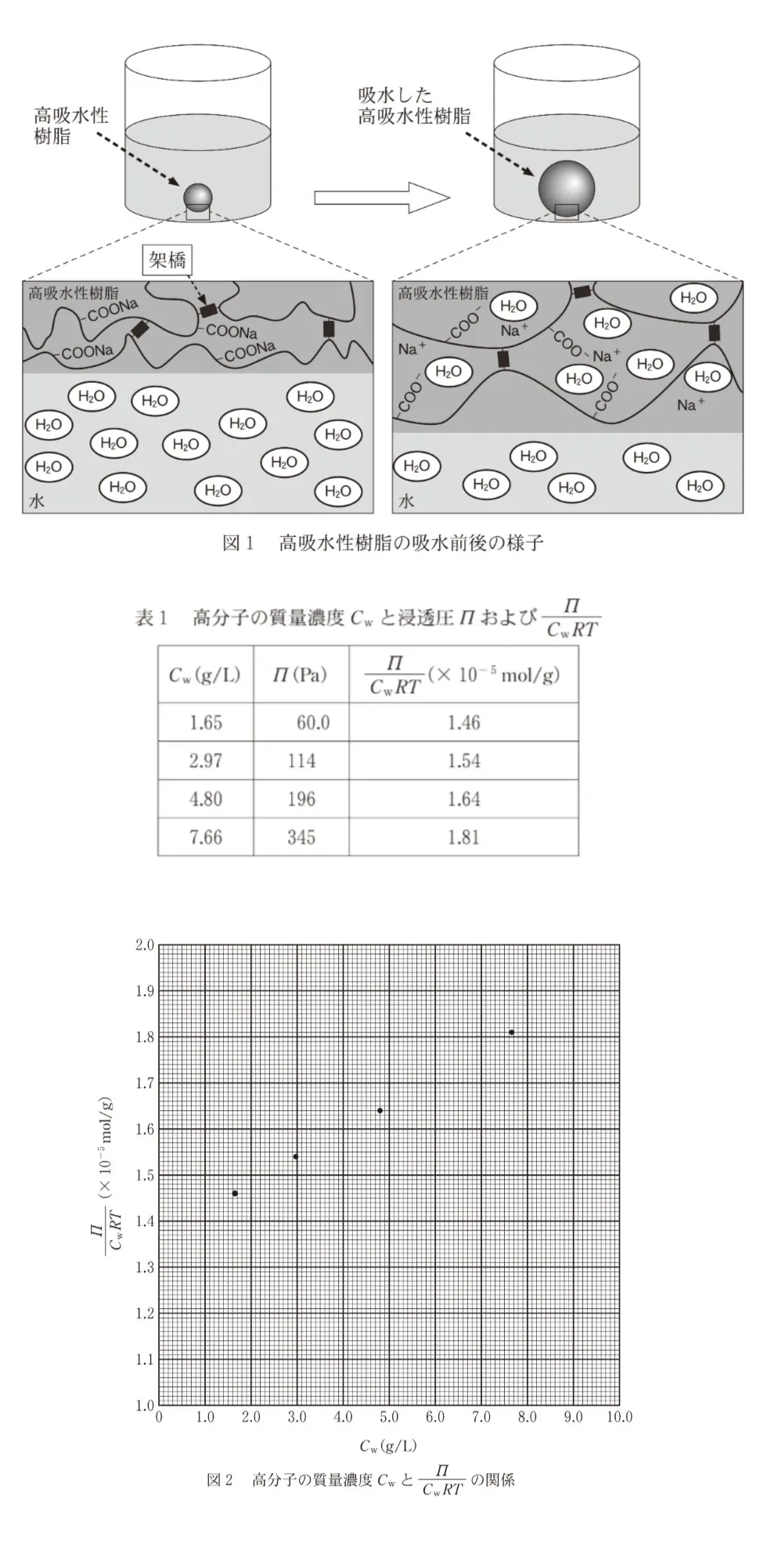
300Kで、ある非電解質の高分子の質量濃度CWを変化させてΠを測定し、Π／CWRTを求めると表1のようになった。表1の値を方眼紙に記入すると、図2のようになる。この高分子のM′はいくらか。最も適当な数値を、後の選択肢のうちから一つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（理科）試験 令和5年度（2023年度）追・再試験 問112（化学（第5問） 問7） （訂正依頼・報告はこちら）
次の文章を読み、後の問いに答えよ。
（a）モノマー間の共有結合だけで網目状の立体構造をつくっている高分子や、架橋構造（橋かけ構造）により網目状の立体構造をつくっている高分子は、機能性高分子などとして身のまわりで多く利用されている。（b）ポリアクリル酸ナトリウムに架橋構造をもたせ、網目状の立体構造となった高分子は、高吸水性樹脂（吸水性高分子）として利用されている。この高吸水性樹脂内部には電離する官能基―COONaが存在する。（c）高吸水性樹脂を水に浸すと、水分子が樹脂の中に吸収され、樹脂の内側と外側でイオン濃度が異なるため浸透圧が生じる。すると水分子がさらに吸収され、網目が広がって図1のように樹脂が膨らむが、分子鎖が共有結合で架橋されているため、樹脂内に一定量の水が保持された状態で吸水がとまる。浸透圧については、希薄溶液では一般にファントホッフの法則が成り立つ。（d）ファントホッフの法則を用いると、浸透圧や溶質の分子量を決定することができる。
下線部（d）に関する次の問いに答えよ。
高分子の溶液では、式（1）は質量濃度CWが小さいときにしか適用できないが、次の式（2）はCWが大きくても適用できる。
Π＝CWRT｛（1／M′）＋ACW｝ （2）
ここで、M′は非電解質の高分子の平均分子量であり、Aは高分子間および高分子と溶媒との間の相互作用の大きさに関係する定数である。
式（2）を変形すると次の式（3）になり、M′を求めることができる。
Π／CWRT＝（1／M′）＋ACW （3）
CWが0に近づくとΠもCWRTも0に近づくが、式（3）が示すように、その比Π／CWRTは1／M′に近づくことを利用する。具体的には、CWが異なるいくつかの試料を調製し、それぞれに対してΠを測定する。得られた結果を用いてCWを横軸に、Π／CWRTを縦軸にとってグラフに表すと、CW＝0での切片からM′を求めることができる。
300Kで、ある非電解質の高分子の質量濃度CWを変化させてΠを測定し、Π／CWRTを求めると表1のようになった。表1の値を方眼紙に記入すると、図2のようになる。この高分子のM′はいくらか。最も適当な数値を、後の選択肢のうちから一つ選べ。
（a）モノマー間の共有結合だけで網目状の立体構造をつくっている高分子や、架橋構造（橋かけ構造）により網目状の立体構造をつくっている高分子は、機能性高分子などとして身のまわりで多く利用されている。（b）ポリアクリル酸ナトリウムに架橋構造をもたせ、網目状の立体構造となった高分子は、高吸水性樹脂（吸水性高分子）として利用されている。この高吸水性樹脂内部には電離する官能基―COONaが存在する。（c）高吸水性樹脂を水に浸すと、水分子が樹脂の中に吸収され、樹脂の内側と外側でイオン濃度が異なるため浸透圧が生じる。すると水分子がさらに吸収され、網目が広がって図1のように樹脂が膨らむが、分子鎖が共有結合で架橋されているため、樹脂内に一定量の水が保持された状態で吸水がとまる。浸透圧については、希薄溶液では一般にファントホッフの法則が成り立つ。（d）ファントホッフの法則を用いると、浸透圧や溶質の分子量を決定することができる。
下線部（d）に関する次の問いに答えよ。
高分子の溶液では、式（1）は質量濃度CWが小さいときにしか適用できないが、次の式（2）はCWが大きくても適用できる。
Π＝CWRT｛（1／M′）＋ACW｝ （2）
ここで、M′は非電解質の高分子の平均分子量であり、Aは高分子間および高分子と溶媒との間の相互作用の大きさに関係する定数である。
式（2）を変形すると次の式（3）になり、M′を求めることができる。
Π／CWRT＝（1／M′）＋ACW （3）
CWが0に近づくとΠもCWRTも0に近づくが、式（3）が示すように、その比Π／CWRTは1／M′に近づくことを利用する。具体的には、CWが異なるいくつかの試料を調製し、それぞれに対してΠを測定する。得られた結果を用いてCWを横軸に、Π／CWRTを縦軸にとってグラフに表すと、CW＝0での切片からM′を求めることができる。
300Kで、ある非電解質の高分子の質量濃度CWを変化させてΠを測定し、Π／CWRTを求めると表1のようになった。表1の値を方眼紙に記入すると、図2のようになる。この高分子のM′はいくらか。最も適当な数値を、後の選択肢のうちから一つ選べ。
- 5.5✕104
- 6.1✕104
- 6.5✕104
- 6.8✕104
- 7.3✕104
正解！素晴らしいです
残念...
この過去問の解説
前の問題（問109）へ
令和5年度（2023年度）追・再試験 問題一覧
次の問題（問113）へ